Unraveling The Mysteries Of The Unit Circle With Trig Identities

The unit circle serves as a fundamental tool in trigonometry, providing a visual representation that simplifies the understanding of trigonometric identities. This circular graph, with a radius of one, is centered at the origin of a coordinate system, making it an essential reference for angles and their corresponding sine, cosine, and tangent values. By exploring the unit circle with trig identities, we can unravel the intricate relationships between these functions, which are vital for solving various mathematical problems in higher education. Understanding these relationships not only aids in grasping the concepts of angles and their measures but also enhances our ability to work with periodic functions.

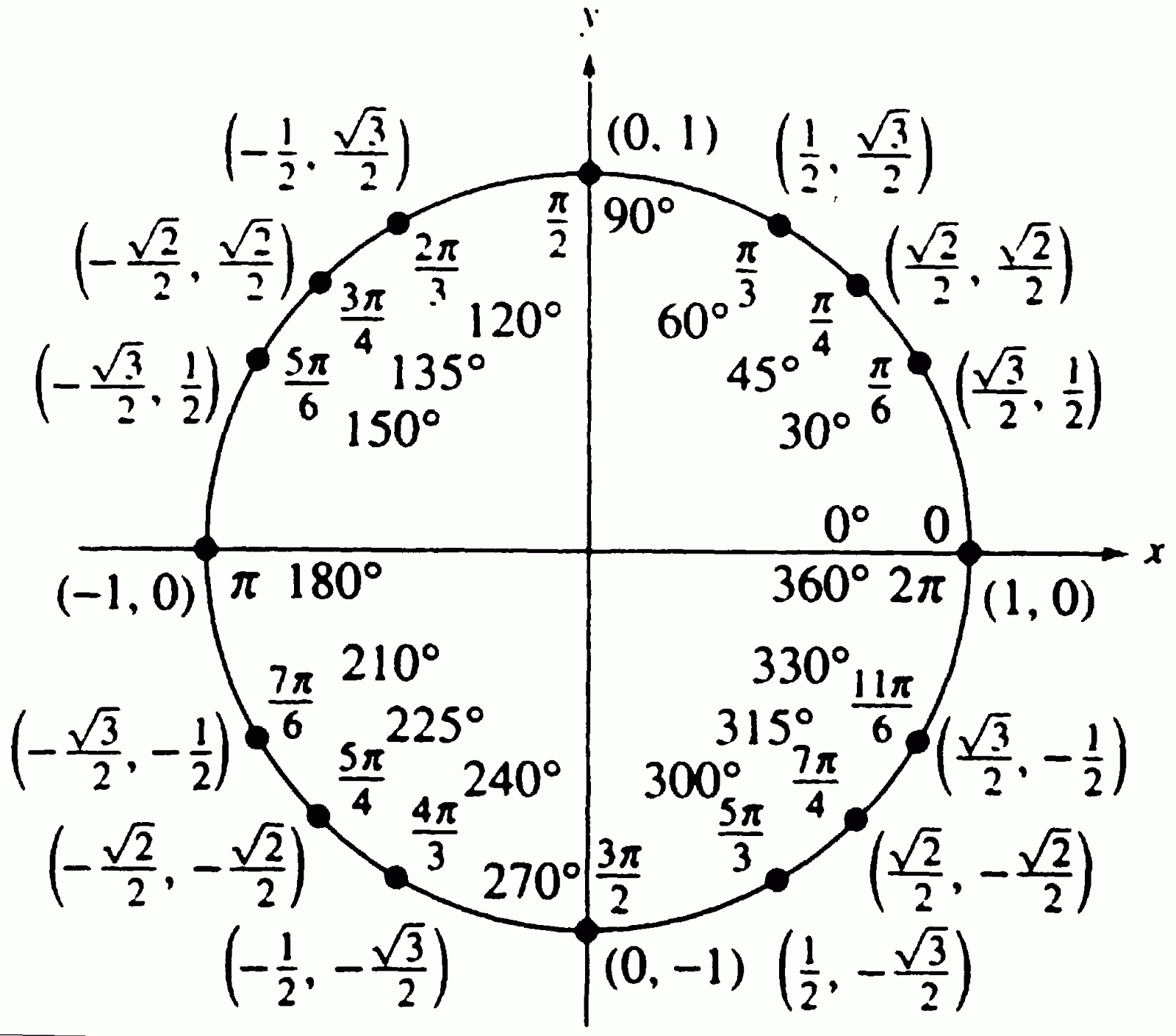
As we delve deeper into the unit circle with trig identities, we will discover how angles in radians and degrees can be interpreted on the circle. The unit circle allows us to easily find the coordinates of points corresponding to specific angles, which can then be used to derive the sine and cosine values. These values are foundational for trigonometric calculations and play a crucial role in various fields such as physics, engineering, and computer science. The beauty of the unit circle lies in its simplicity, providing a straightforward approach to understanding complex trigonometric relationships.

Students often find trigonometry challenging, but with the unit circle and its associated identities, learning becomes more accessible. By visualizing angles and their corresponding functions, we can demystify the topic and pave the way for a deeper comprehension of mathematical principles. This article will guide you through the essential aspects of the unit circle with trig identities, helping you appreciate its significance in both theoretical and applied mathematics.

What is the Unit Circle?

The unit circle is defined as a circle with a radius of one, centered at the origin of the Cartesian coordinate system. It serves as a reference for angles measured in both degrees and radians. The equation of the unit circle is given by:

x² + y² = 1

Each point (x, y) on the unit circle corresponds to an angle θ, where:

x = cos(θ) and y = sin(θ)

This relationship establishes a direct link between the coordinates of points on the circle and the trigonometric functions sine and cosine.

How Do Angles Relate to the Unit Circle with Trig Identities?

When exploring the unit circle, we can represent angles in both degrees and radians. A complete rotation around the circle corresponds to 360 degrees or 2π radians. Here are some key angles and their corresponding coordinates:

0° (0 radians): (1, 0)
90° (π/2 radians): (0, 1)
180° (π radians): (-1, 0)
270° (3π/2 radians): (0, -1)
360° (2π radians): (1, 0)

These coordinates allow us to easily derive the sine and cosine values for each angle, which are essential for various trigonometric calculations.

What are the Key Trig Identities Derived from the Unit Circle?

The unit circle provides a foundation for several important trigonometric identities, including:

Pythagorean Identity: sin²(θ) + cos²(θ) = 1
Reciprocal Identities:
- csc(θ) = 1/sin(θ)
- sec(θ) = 1/cos(θ)
- cot(θ) = 1/tan(θ)
Quotient Identities:
- tan(θ) = sin(θ)/cos(θ)
- cot(θ) = cos(θ)/sin(θ)

These identities are crucial for simplifying trigonometric expressions and solving equations.

How Can We Visualize Trigonometric Functions Using the Unit Circle?

The unit circle allows us to visualize the behavior of trigonometric functions over a complete cycle. As we move around the circle, the sine and cosine functions oscillate between -1 and 1, creating a periodic wave pattern. Below is a summary of how these functions behave:

As θ increases from 0 to 90°, sin(θ) increases from 0 to 1, while cos(θ) decreases from 1 to 0.
From 90° to 180°, sin(θ) remains at 1, and cos(θ) becomes negative.
From 180° to 270°, sin(θ) decreases to -1, and cos(θ) stays negative.
From 270° back to 360°, sin(θ) returns to 0, and cos(θ) returns to 1.

This cyclical nature of the unit circle with trig identities offers a clear insight into the behavior of sine and cosine functions.

What Are the Applications of the Unit Circle in Real Life?

The unit circle and trigonometric identities are not only important for theoretical mathematics but also have practical applications in various fields:

Physics: Trigonometric functions model oscillations, waves, and other periodic phenomena.
Engineering: Trigonometry is used in designing structures, analyzing forces, and understanding mechanics.
Computer Science: Trigonometric algorithms are essential in graphics, animation, and game design.
Navigation: Trigonometry is used in calculating distances and angles for map reading and GPS technology.

The versatility of the unit circle with trig identities highlights its significance across various disciplines.

How Can Students Master the Unit Circle with Trig Identities?

Mastering the unit circle and its associated trig identities requires practice and a solid understanding of the foundational concepts. Here are some effective strategies:

Visualization: Draw the unit circle and label key angles and coordinates.
Practice: Solve problems involving trigonometric identities and equations.
Use Mnemonics: Create memory aids to remember key identities and their relationships.
Group Study: Collaborate with peers to discuss and solve trigonometric problems.

By employing these strategies, students can enhance their understanding and application of the unit circle with trig identities.

Conclusion: Why is the Unit Circle Essential for Understanding Trigonometry?

The unit circle is a powerful tool that lays the groundwork for understanding trigonometric functions and identities. By visualizing angles and their corresponding sine and cosine values, we can simplify complex calculations and solve problems more efficiently. The unit circle with trig identities is not just a theoretical concept; it has real-world applications that span various fields, making it an essential topic for students and professionals alike. Embracing the unit circle will empower learners to navigate the world of trigonometry with confidence and clarity.