Understanding The Equation Of A Normal Line: A Deep Dive Into Geometry

The equation of a normal line is a fundamental concept in geometry and calculus, serving as a vital tool for students and professionals alike. This mathematical principle not only helps in understanding the behavior of curves and surfaces but also finds applications in various fields, from engineering to physics. In this article, we will explore the intricacies of the equation of a normal line, its derivation, and its significance in mathematical analysis.

When we discuss the equation of a normal line, we are referring to a line that is perpendicular to a given curve at a specific point. This line stands in contrast to the tangent line, which touches the curve at that same point and shares the same slope. Understanding the relationship between normal lines and tangent lines is crucial for a comprehensive grasp of differential calculus. In this exploration, we will delve into the methods of finding the equation of a normal line and the practical implications of this knowledge.

Furthermore, the equation of a normal line plays an essential role in optimizing functions, determining maximum and minimum values, and analyzing the properties of curves. As we move through this article, we will address common questions related to normal lines, provide examples, and illustrate the step-by-step process of deriving these equations. Whether you are a student seeking clarity or a professional looking to refresh your knowledge, this guide will serve as an invaluable resource.

What is the Equation of a Normal Line?

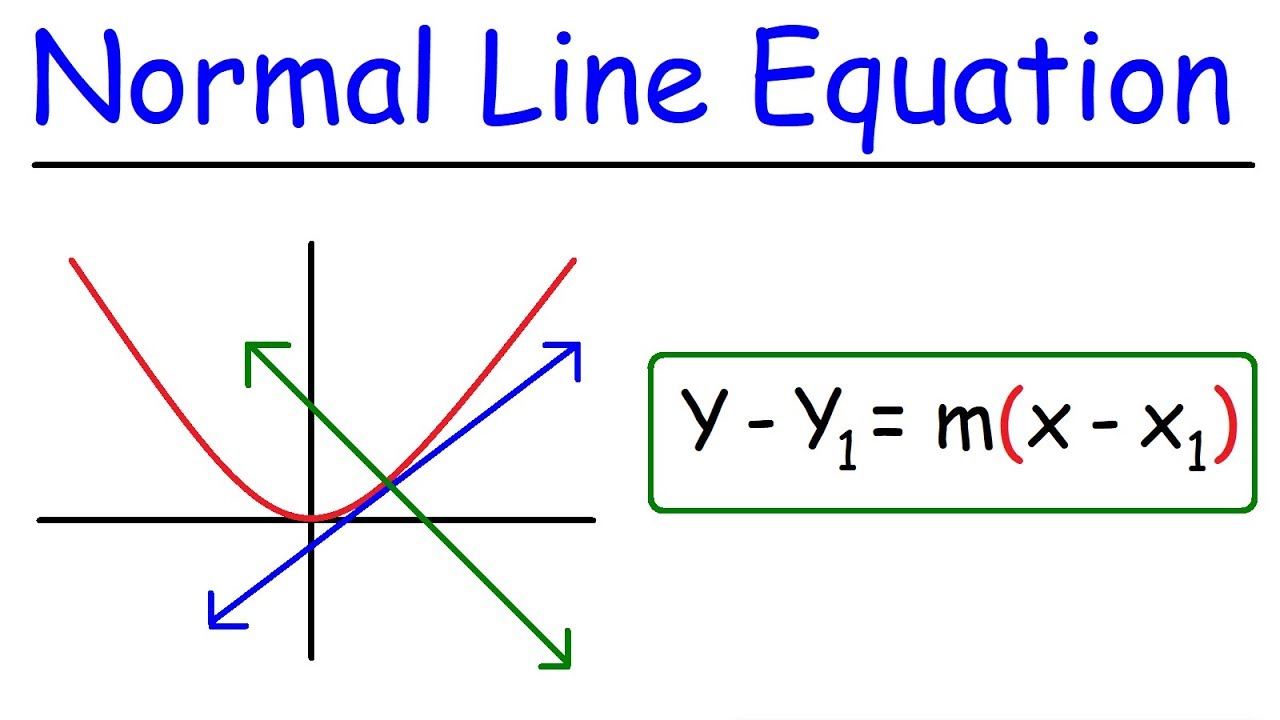
The equation of a normal line refers to the mathematical representation of a line that is perpendicular to a curve at a particular point. To understand this better, consider a function f(x) defined in a Cartesian plane. If we identify a point (a, f(a)) on this curve, the normal line at that point can be determined using its slope and the coordinates of the point. The slope of the normal line is the negative reciprocal of the slope of the tangent line at that point.

How to Derive the Equation of a Normal Line?

To derive the equation of a normal line, follow these steps:

1. Identify the point on the curve where you want to find the normal line.
2. Calculate the derivative of the function at that point to find the slope of the tangent line.
3. Determine the slope of the normal line by taking the negative reciprocal of the tangent slope.
4. Use the point-slope form of the line equation to write the equation of the normal line.

Example of Finding the Equation of a Normal Line

Let’s consider the function f(x) = x². We want to find the equation of the normal line at the point (1, 1).

1. Find the derivative of f(x): f'(x) = 2x.
2. Evaluate the derivative at x = 1: f'(1) = 2(1) = 2 (slope of the tangent line).
3. The slope of the normal line is the negative reciprocal: m_normal = -1/2.
4. Using the point-slope form: y - 1 = -1/2(x - 1), which simplifies to y = -1/2x + 3/2.

Why is the Equation of a Normal Line Important?

The equation of a normal line is significant for several reasons:

• It helps in understanding the geometric properties of curves.
• It is used in optimization problems in calculus.
• It aids in the analysis of motion in physics.
• It provides insights into the behavior of functions around specific points.

What are the Applications of Normal Lines in Real Life?

Normal lines are not just theoretical constructs; they have practical applications in various fields:

• Engineering: Designing structures that require precise measurements and calculations.
• Physics: Analyzing trajectories and forces acting on objects.
• Computer Graphics: Rendering curves and surfaces accurately in 3D modeling.

How Does the Equation of a Normal Line Relate to Tangent Lines?

The relationship between normal lines and tangent lines is critical in calculus. While the tangent line provides the best linear approximation of a curve at a point, the normal line provides a way to understand how the curve behaves in a perpendicular direction. This duality is essential in optimization, as it helps identify points of interest, such as local maxima and minima.

Can the Equation of a Normal Line be Extended to Higher Dimensions?

Yes, the concept of a normal line can be extended to higher dimensions. In three-dimensional space, for example, a normal vector can be defined at a point on a surface, which is perpendicular to the tangent plane at that point. The equation of the normal line in 3D can be formulated similarly to the 2D case, considering the partial derivatives of the surface function.

Conclusion: Mastering the Equation of a Normal Line

In summary, the equation of a normal line is a vital concept in mathematics that bridges the gap between geometry and calculus. By understanding how to derive and apply this equation, students and professionals can enhance their analytical skills and deepen their comprehension of mathematical principles. As you continue to explore the fascinating world of curves and surfaces, the knowledge of normal lines will undoubtedly prove to be a valuable asset in your mathematical toolkit.