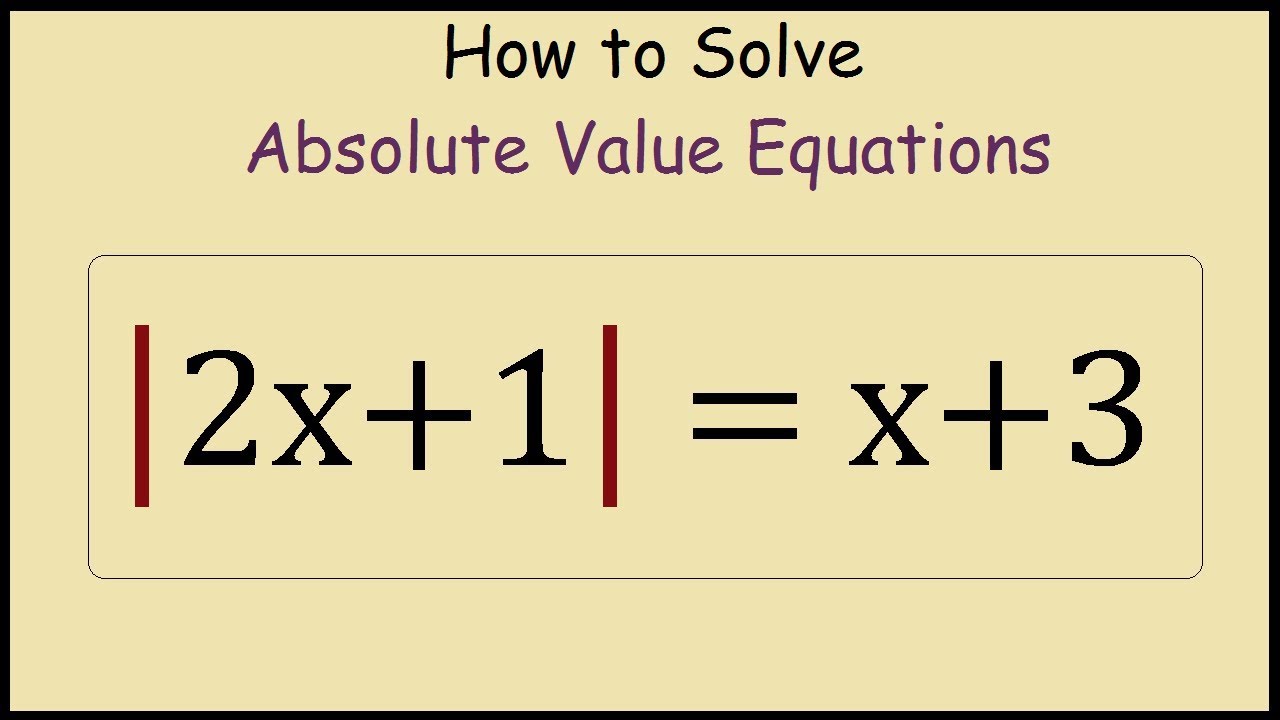Understanding When It Happens In An Absolute Value Equation
When grappling with the intricacies of mathematics, particularly in algebra, one might encounter the concept of absolute value equations. These equations play a crucial role in understanding distance on a number line, and they often lead to fascinating discussions about solutions and their implications. But what exactly is an absolute value equation, and when does it happen that we need to solve for them? This article aims to delve deep into the nuances of absolute value equations, providing clarity and insight into this essential mathematical concept.
One of the first things to understand about absolute value equations is that they can present unique challenges that require a specific approach to solve. The absolute value of a number is its distance from zero, regardless of direction. Therefore, when an equation involves an absolute value, it can lead to two possible scenarios for solutions. This duality is what makes absolute value equations particularly intriguing and important in the realm of mathematics.
Throughout this article, we will explore various aspects of absolute value equations, including their definition, how to solve them, common problems encountered, and insights on their applications. By the end of this discussion, readers will have a comprehensive understanding of when it happens in an absolute value equation, enabling them to tackle such problems with confidence and skill.
What is an Absolute Value Equation?
An absolute value equation is defined as an equation that includes an absolute value expression. The general form of such an equation is |x| = a, where x is the variable and a is a non-negative real number. The absolute value function outputs the distance of a number from zero, which can either be positive or negative.
How Do You Solve Absolute Value Equations?
To solve an absolute value equation, it's essential to recognize that there are two cases to consider:
- Case 1: The expression inside the absolute value is equal to the positive value, i.e., x = a.
- Case 2: The expression inside the absolute value is equal to the negative value, i.e., x = -a.
As a result, each absolute value equation can lead to two potential solutions. For instance, if we consider the equation |x| = 3, the solutions would be x = 3 and x = -3.
When Does It Happen in an Absolute Value Equation?
Understanding when solutions arise in an absolute value equation is crucial for solving such equations effectively. It occurs when the equation is set equal to a non-negative number. However, if the equation is set to a negative number, there will be no solution since absolute values cannot produce negative outputs.
What Are Common Mistakes When Solving Absolute Value Equations?
Students often make several common mistakes when dealing with absolute value equations. Some of these include:
- Ignoring the two cases that arise from the absolute value.
- Assuming that |x| = -a can yield valid solutions.
- Failing to check solutions in the original equation.
These oversights can lead to incorrect conclusions, so it’s vital to approach such equations with caution and thoroughness.
Can Absolute Value Equations Have No Solutions?
Yes, absolute value equations can have no solutions. This occurs specifically when the equation is set equal to a negative number. For example, the equation |x| = -2 has no solutions since absolute values cannot equal a negative quantity.
How Are Absolute Value Equations Used in Real Life?
Absolute value equations are not just abstract concepts; they have practical applications in various fields, such as:
- Physics: Calculating distances and speeds.
- Engineering: Analyzing forces and loads.
- Economics: Measuring deviations from expected values.
Recognizing the real-world relevance of absolute value equations can enhance a student’s understanding and appreciation of the subject.
What Are Some Examples of Absolute Value Equations?
Let’s consider a few examples of absolute value equations and their solutions:
- Example 1: |x - 4| = 5
- Case 1: x - 4 = 5 → x = 9
- Case 2: x - 4 = -5 → x = -1
Solutions: x = 9 and x = -1. - Example 2: |2x + 3| = 7
- Case 1: 2x + 3 = 7 → 2x = 4 → x = 2
- Case 2: 2x + 3 = -7 → 2x = -10 → x = -5
Solutions: x = 2 and x = -5.
Conclusion: Mastering Absolute Value Equations
In conclusion, understanding when it happens in an absolute value equation is fundamental to mastering algebra. By recognizing the structure of these equations, the method of solving them, and the potential pitfalls, students can confidently approach and solve absolute value equations. This understanding not only improves mathematical skills but also opens the door to real-world applications and further academic pursuits.
With practice and attention to detail, anyone can become adept at dealing with absolute value equations and appreciate their importance in both academic settings and everyday life.