How To Find The Area Of A Polygon: A Comprehensive Guide

Finding the area of a polygon is a fundamental concept in geometry that has practical applications in various fields such as architecture, engineering, and land surveying. Understanding how to calculate the area of different types of polygons can help you make informed decisions in both academic and real-world scenarios. In this article, we will explore various methods and formulas used to find the area of polygons, including triangles, quadrilaterals, and more complex shapes.

Not only will we cover the mathematical principles behind these calculations, but we will also provide tips and tricks to simplify the process. Whether you are a student looking to improve your math skills or a professional needing to apply these concepts in your work, this guide is designed to be accessible and informative.

As you delve into this topic, you will discover the importance of precision in measurements and the role they play in calculating area accurately. We will provide examples and practical applications to ensure that you can apply what you've learned effectively. Let’s get started!

Table of Contents

• What is a Polygon?
• Types of Polygons
• Formula for Area of Polygons
• Finding Area of Triangles
• Finding Area of Quadrilaterals
• Finding Area of Regular Polygons
• Using Coordinates to Find Area
• Practical Applications
• Conclusion

What is a Polygon?

A polygon is a closed two-dimensional shape formed by a finite number of straight line segments connected end-to-end. These line segments are referred to as sides, while the points where they meet are called vertices. Polygons can be classified based on the number of their sides and the angles between them.

Types of Polygons

Polygons can be categorized into several types, including:

• Triangles: 3 sides
• Quadrilaterals: 4 sides
• Pentagons: 5 sides
• Hexagons: 6 sides
• Heptagons: 7 sides
• Octagons: 8 sides
• Decagons: 10 sides

Regular vs. Irregular Polygons

Polygons can also be classified as regular or irregular:

• Regular Polygons: All sides and angles are equal.
• Irregular Polygons: Sides and angles are not equal.

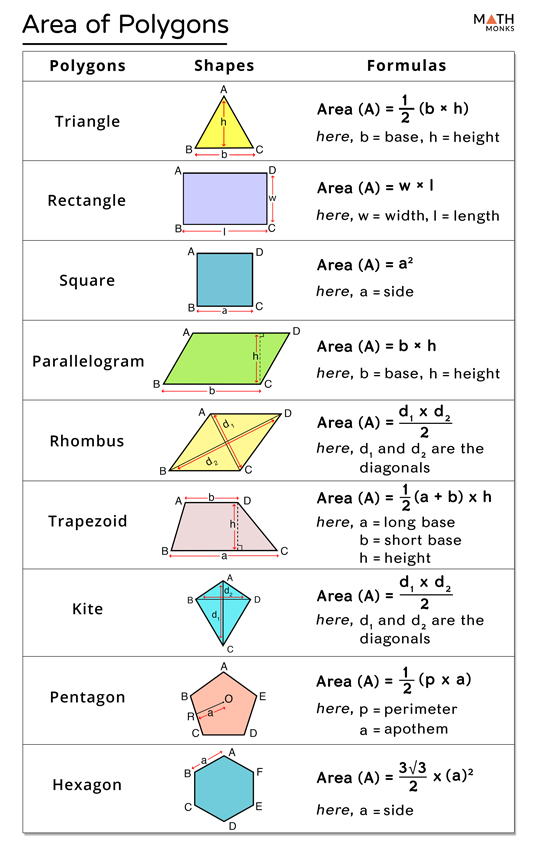
Formula for Area of Polygons

The formula used to calculate the area of a polygon depends on its type. Below are some general formulas:

Area of Triangle

The area (A) of a triangle can be calculated using the formula:

A = 1/2 * base * height

Area of Quadrilateral

The area of a quadrilateral can be calculated using various formulas based on the type of quadrilateral:

• For rectangles: A = length * width
• For squares: A = side²
• For trapezoids: A = 1/2 * (base1 + base2) * height

Finding Area of Triangles

To find the area of a triangle, you need to know the base and the height. Here’s how to do it:

• Measure the base of the triangle.
• Measure the height from the base to the opposite vertex.
• Substitute the values into the formula: A = 1/2 * base * height.

For example, if the base is 10 units and the height is 5 units, the area would be:

A = 1/2 * 10 * 5 = 25 square units.

Finding Area of Quadrilaterals

Quadrilaterals have different methods for calculating area based on their shape.

Finding Area of Rectangles

For rectangles, simply multiply the length by the width:

A = length * width

Finding Area of Trapezoids

For trapezoids, use the formula:

A = 1/2 * (base1 + base2) * height

Example: If base1 is 8 units, base2 is 5 units, and the height is 4 units, then:

A = 1/2 * (8 + 5) * 4 = 26 square units.

Finding Area of Regular Polygons

For regular polygons, the area can be calculated using the formula:

A = (1/4) * n * s² / tan(π/n)

Where n is the number of sides and s is the length of a side.

For example, for a regular hexagon with a side length of 6 units:

A = (1/4) * 6 * 6² / tan(π/6) = 15.588 square units.

Using Coordinates to Find Area

For polygons defined by vertices in a coordinate plane, the area can be calculated using the Shoelace Theorem:

A = 1/2 * | Σ (x_iy_i+1 - x_i+1y_i) |

Where (x_i, y_i) are the coordinates of the vertices.

This method is particularly useful for irregular polygons.

Practical Applications

Understanding how to find the area of polygons is valuable in various fields, including:

• Architecture: Calculating material quantities and space design.
• Land Surveying: Determining land ownership and property boundaries.
• Urban Planning: Designing parks and public spaces.

Conclusion

In summary, calculating the area of a polygon involves understanding its type and applying the appropriate formulas. From triangles to regular polygons, each shape has its unique method for area calculation. By mastering these methods, you can apply this knowledge in both academic and practical contexts.

We encourage you to practice these calculations and explore further resources to deepen your understanding. If you found this article helpful, please leave a comment or share it with others interested in geometry!