Linear Vs Nonlinear On A Plot: Understanding The Differences

Linear vs Nonlinear on a plot is a fundamental concept in mathematics and data visualization that helps us understand the relationship between variables. In this article, we will explore the key differences between linear and nonlinear plots, how to interpret them, and the significance of each in various fields such as science, engineering, and economics. Understanding these concepts is crucial for anyone looking to analyze data effectively and make informed decisions based on visual representations.

The distinction between linear and nonlinear relationships can greatly influence how we interpret data. Linear relationships depict a constant rate of change, while nonlinear relationships can exhibit varying rates of change. This article aims to clarify these concepts with detailed examples, charts, and relevant applications that demonstrate their importance in real-world scenarios.

By the end of this article, you will have a comprehensive understanding of linear vs nonlinear plots, enabling you to apply this knowledge in your data analysis and visualization tasks. Let's dive into the world of plotting and discover how these two types of relationships shape our understanding of data.

Definition of Linear and Nonlinear Relationships
Characteristics of Linear Plots
Characteristics of Nonlinear Plots
Examples of Linear vs Nonlinear Relationships
Applications in Various Fields
Visualization Techniques for Linear and Nonlinear Data
Challenges in Analyzing Nonlinear Data
Conclusion and Takeaways

Definition of Linear and Nonlinear Relationships

A linear relationship between two variables can be described by a straight line on a graph. The general form of a linear equation is:

y = mx + b

Where:

y = dependent variable
x = independent variable
m = slope of the line
b = y-intercept

On the other hand, a nonlinear relationship does not follow a straight line and can take various forms, such as quadratic, exponential, or logarithmic functions. Nonlinear equations are generally more complex and can be represented as:

y = f(x)

Where f(x) is a nonlinear function of x.

Characteristics of Linear Plots

Linear plots have several defining characteristics:

Constant Rate of Change: The slope of the line remains constant across the entire range of data.
Simplicity: Linear equations are straightforward and easy to interpret.
Predictability: Linear relationships allow for easy predictions of outcomes based on changes in the independent variable.

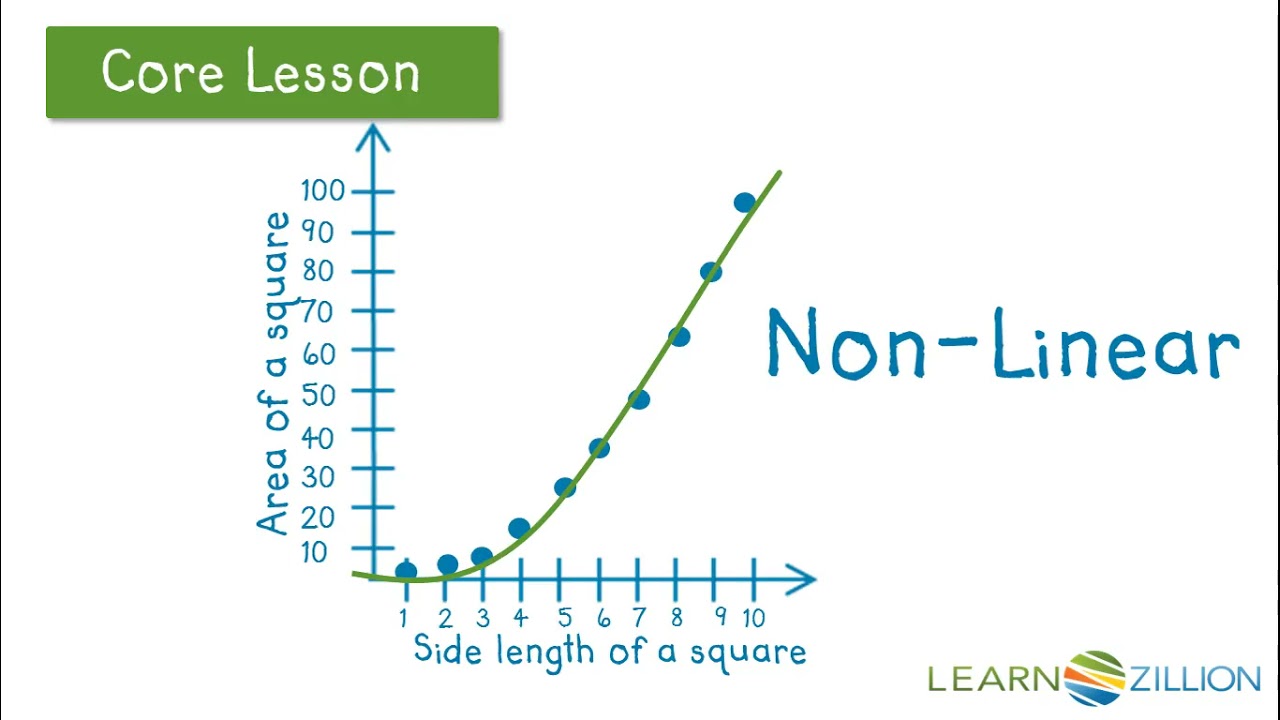
Characteristics of Nonlinear Plots

Nonlinear plots exhibit different characteristics:

Variable Rate of Change: The slope can vary significantly, leading to different rates of increase or decrease.
Complexity: Nonlinear equations can involve more complicated terms, making them harder to interpret.
Multiple Trends: Nonlinear relationships can show several trends within the same dataset.

Examples of Linear vs Nonlinear Relationships

To better understand the differences, let's look at some practical examples:

Linear Example

A classic example of a linear relationship is the conversion of Celsius to Fahrenheit:

F = (9/5)C + 32

This relationship produces a straight line when plotted, showing a constant rate of change as the temperature increases.

Nonlinear Example

An example of a nonlinear relationship is the growth of bacteria over time, which can be represented by an exponential function:

N(t) = N0 * e^(rt)

Where N0 is the initial quantity, r is the growth rate, and t is time. This relationship results in a curve that steepens as time progresses.

Applications in Various Fields

Understanding linear and nonlinear relationships is crucial across multiple disciplines:

Science: In biology, nonlinear models are often used to represent population growth.
Economics: Linear models are used in demand and supply curves, while nonlinear models can represent consumer behavior.
Engineering: Linear equations are used in structural analysis, whereas nonlinear equations are essential for complex simulations.

Visualization Techniques for Linear and Nonlinear Data

Choosing the right visualization technique is vital for effectively communicating data:

Linear Data: Use scatter plots with a line of best fit to represent linear relationships.
Nonlinear Data: Employ scatter plots with curves or polynomial regression lines to depict nonlinear trends.

Challenges in Analyzing Nonlinear Data

Nonlinear data analysis poses several challenges:

Complexity: The need for advanced mathematical models can complicate analysis.
Interpretation: Nonlinear relationships can be difficult to interpret without proper tools.
Data Overfitting: Fitting a model too closely to data can result in overfitting, reducing predictive power.

Conclusion and Takeaways

In summary, understanding the differences between linear and nonlinear plots is essential for effective data analysis. Linear relationships provide simplicity and predictability, while nonlinear relationships offer complexity and depth. Recognizing when to apply each type of relationship can significantly enhance your analytical capabilities.

We encourage you to engage with this topic further by leaving comments, sharing your thoughts, or exploring related articles on our site.

Thank you for reading! We hope this article has provided you with valuable insights into linear vs nonlinear on a plot, and we look forward to seeing you again for more informative content.